Suppose the wealth that is to be received at a time \(T\) in the future has the form

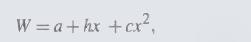
where \(a\) is a constant and \(x\) is a random variable. The value of the variable \(h\) can be selected by the investor. Suppose that the investor has a utility function that is increasing and strictly concave. Suppose also that the probability distribution of \(x\) is symmetric; that is, \(x\) and \(-x\)

have the same distribution. It follows that \(\mathrm{E}(x)=0\) and that the investor cannot influence the expected value of wealth.

(a) Show that the optimal choice is \(h=0\).

(b) Apply this result to the corn farm problem to show that the optimal futures position is \(+4,000\).

Transcribed Image Text:

W = a+hx + cx,