The IRR is generally calculated using an iterative procedure. Suppose that we define (f(lambda)=-a_{0}+a_{1} lambda+a_{2} lambda^{2}+cdots+a_{n} lambda^{n}),
Question:
The IRR is generally calculated using an iterative procedure. Suppose that we define \(f(\lambda)=-a_{0}+a_{1} \lambda+a_{2} \lambda^{2}+\cdots+a_{n} \lambda^{n}\), where all \(a_{i}\) 's are positive and \(n>1\). Here is an iterative technique that generates a sequence \(\lambda_{0}, \lambda_{1}, \lambda_{2}, \ldots, \lambda_{k}, \ldots\) of estimates that converges to the root \(\bar{\lambda}>0\), solving \(f(\bar{\lambda})=0\). Start with any \(\lambda_{0}>0\) close to the solution. Assuming \(\lambda_{k}\) has been calculated, evaluate
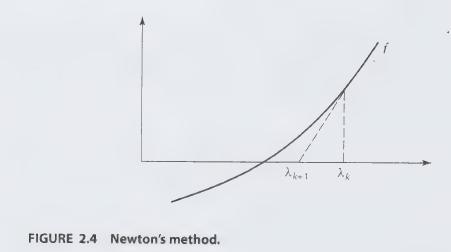
This is Newton's method. It is based on approximating the function \(f\) by a line tangent to its graph at \(\lambda_{k}\), as shown in Figure 2.4. Try the procedure on \(f(\lambda)=-1+\lambda+\lambda^{2}\). Start with \(\lambda_{0}=1\) and compute four additional estimates.
Step by Step Answer:
This question has not been answered yet.
You can Ask your question!
