We showed in Eq. (2.10) that S = I + CA, where S is national saving, I is investment, and CA is the current account balance. Calculations of national saving and investment depend on the treatment of government investment. In the text, we treated government purchases, G, as if they were consumption expenditures. Therefore, Eq. (2.7) states that government saving is S_govt = (T - TR - INT) - G, so that (1) national saving in Eq. (2.8) is S = Y + NFP - C - G, and (2) I in Eq. (2.10) is gross private domestic investment GPDI. As mentioned in the text, a more detailed treatment recognizes that government purchases comprise consumption expenditures, which we will call GCE, and government investment, which we will call GI, so G = GCE + GI. Now define government saving as (T - TR - INT) - GCE. With this alternative definition of government saving, show that private saving plus government saving = I + CA, where investment (I) is the sum of GPDI and GI. Table 5.1, titled “Saving and Investment by Sector,” in the National Income and Product Accounts (found online at www.bea.gov) uses this more detailed treatment. For the most recent quarter for which all data in Table 5.1 are available, what are the values of gross saving, gross domestic investment (gross private domestic investment plus gross government investment), and the current account balance (shown in Table 5.1 as “Net lending or net borrowing”)? Does the identity hold true? If not, how can the entries for capital account transactions and statistical discrepancy in Table 5.1 help?

S = I + CA (2.10)

S_govt = net government income - government purchases 

= 1T - TR - INT2 - G. (2.7)

S = Spvt + Sgovt 

= 1Y + NFP - T + TR + INT - C2 + 1T - TR - INT - G2 

= Y + NFP - C - G. (2.8) 

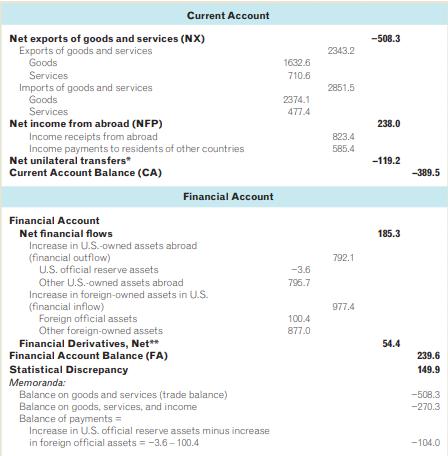
Table 5.1:

Transcribed Image Text:

Current Account Net exports of goods and services (NX) Exports of goods and services Goods Services Imports of goods and services Goods Services Net income from abroad (NFP) Income receipts from abroad Income payments to residents of other countries Net unilateral transfers* Current Account Balance (CA) Financial Account -508.3 2343.2 1632.6 710.6 2851.5 2374.1 477.4 238.0 823.4 585.4 -119.2 -389.5 Financial Account Net financial flows 185.3 Increase in U.S.-owned assets abroad (financial outflow) 792.1 U.S. official reserve assets -3.6 Other U.S.-owned assets abroad 796.7 Increase in foreign-owned assets in U.S. (financial inflow) 977.4 Foreign official assets Other foreign-owned assets 100.4 877.0 Financial Derivatives, Net** Financial Account Balance (FA) Statistical Discrepancy 54.4 239.6 149.9 Memoranda: Balance on goods and services (trade balance) -508.3 Balance on goods, services, and income -270.3 Balance of payments = Increase in U.S. official reserve assets minus increase in foreign official assets = -3.6-100.4 -104.0