1. We have developed a diagnostic system with three possible diagnoses, Q, R, and S, that are equally probable (0.333 each). Assume that the costs associated with the three diagnoses are x, 2x, and 5x, respectively, and that the raw cost matrix comprises the base costs on the diagonal and the sum of the row and column values for off-diagonal values, as illustrated in Table 10.7. (For example, Q misdiagnosed as S costs x + 5x, and so on.) Actually, the cost of condition S is 10x, but we are reimbursed 50 percent of the cost by Medicare, so our cost is 5x, and Table 10.7 is valid. Assume that, despite the cost differences in diagnosing the conditions, each diagnosis represents a relatively mild problem and none is more healththreatening than any other; that is, none is more serious than a common cold.

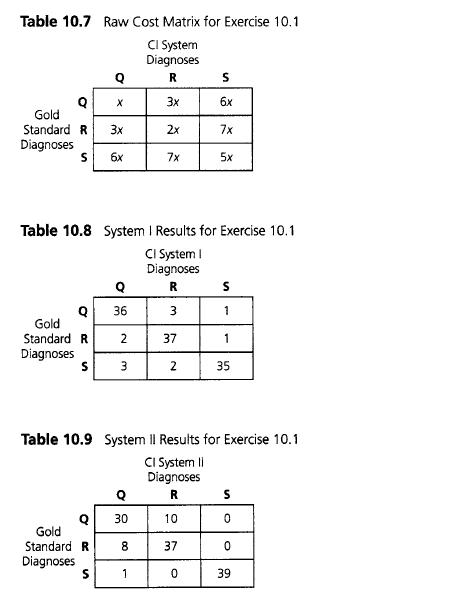
Further assume that we have trained two computational intelligence diagnostic systems, I and II, and the results are evaluated using the 40 cases of each diagnosis we have for testing with the results, as shown in Tables 10.8 and 10.9.
How many patients are misdiagnosed in each case? Purely based on cost, which of the two systems should be used? Assuming x is $20, what are the estimated cost savings in 1,000 cases?
Now assume that the federal government announces that it will stop reimbursing us for S, so that our cost for correctly diagnosing S suddenly doubles to 10x. (Off-diagonal costs must be adjusted accordingly as well.) From a cost perspective, which diagnostic system should we use now? Why? Comment on this method of selecting the diagnostic system.

Transcribed Image Text:

Table 10.7 Raw Cost Matrix for Exercise 10.1 CI System Diagnoses Q R S Q X 3x 6 Gold Standard R 3x 2x 7x Diagnoses S 6x 7x 5x Table 10.8 System I Results for Exercise 10.1 CI System I Diagnoses Q R S Q 36 3 1 Gold Standard R 2 37 1 Diagnoses S 3 2 35 Table 10.9 System II Results for Exercise 10.1 CI System li Diagnoses Q R S Q 30 10 0 Gold Standard R. Diagnoses 00 8 37 0 S 1 0 39