For the special class of utility functions u(w) = w ? be?aw, with a, b > 0, Bell (1988) suggested another measure of risk aversion. For this class, expected utility takes the form

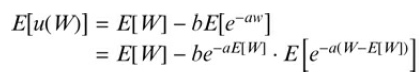
where the product on the right hand side contains a?scaling factor be^?aE[W] and Bell?s risk aversion term. Show that E[e^-a(w-e|W)] does not only take the variance into account, but all higher central moments Mk of the probability distribution of W.

Transcribed Image Text:

E[u(W)] = E[W] – bE[e¯a"] = E[W] – be-aE\W\ . E e-«w-E\WD|