In the article “On Judging the Significance of Differences by Examining the Overlap Between Confidence Intervals,” by Schenker and Gentleman (American Statistician, Vol. 55, No. 3), the authors consider sample data in this statement: “Independent simple random samples, each of size 200, have been drawn, and 112 people in the first sample have the attribute, whereas 88 people in the second sample have the attribute.”

a. Use the methods of this section to construct a 95% confidence interval estimate of the difference p₁ - p₂. What does the result suggest about the equality of p₁ and p₂?
b. Use the methods of Section 7-1 to construct individual 95% confidence interval estimates for each of the two population proportions. After comparing the overlap between the two confidence intervals, what do you conclude about the equality of p₁ and p₂?
c. Use a 0.05 significance level to test the claim that the two population proportions are equal. What do you conclude?
d. Based on the preceding results, what should you conclude about the equality of p₁ and p₂? Which of the three preceding methods is least effective in testing for the equality of p₁ and p₂?

Data From Section 7-1:

The confidence level is the probability 1 - α (such as 0.95, or 95%) that the confidence interval actually does contain the population parameter, assuming that the estimation process is repeated a large number of times. (The confidence level is also called the degree of confidence, or the confidence coefficient.)

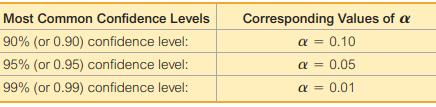
The following table shows the relationship between the confidence level and the corresponding value of α. The confidence level of 95% is the value used most often.