Let P(x,t; x₀,t₀) denote the transition density function of the restricted Brownian process W^μ_t = μt + σZ_t with two absorbing barriers at x = 0 and x = ℓ. Using the method of separation of variables (Kevorkian, 1990), show that the solution to P(x, t; x₀, t₀) admits the following eigen-function expansion [which differs drastically in analytic form from that in (4.1.48)]

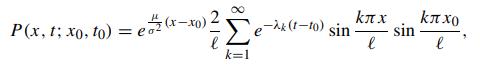
where the eigenvalues are given by

P(x, t; x₀, t₀) satisfies the forward Fokker–Planck equation with auxiliary conditions: P(0,t) = P(ℓ, t) = 0 and P(x, t⁺₀ ; x₀, t₀) = δ(x−x₀). 

Pelsser (2000) derived the above solution by performing the Laplace inversion using Bromwich contour integration. 

Transcribed Image Text:

P(x, f; xo, to) (-1 -10) l Σe-k(-10) sin k=1 κπ - sin kππο l