Let u (x, t) denote the solution to the partial differential equation with u(x, 0 +

Let u^μ(x, t) denote the solution to the partial differential equation

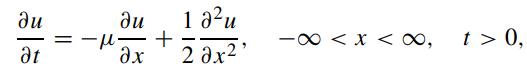with u(x, 0⁺) = δ(x). From (2.3.12), it is seen that 

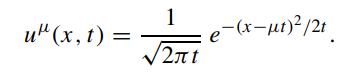
By applying the change of variable: x = y + μt, show that the above equation becomes

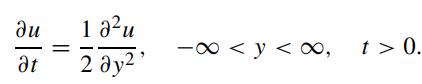
With the initial condition: u(y, 0) = δ(y). The new solution is given by 

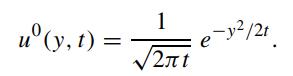
We observe the following relation between u⁰(y, t) and u⁰(x, t):

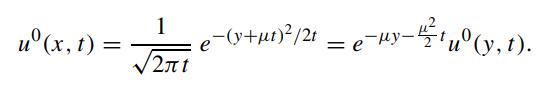
Relate the above result to the Girsanov Theorem. 

Transcribed Image Text:

ди at ди = -н - + ax - 1 02и 2 дх2 -∞0 < x < ∞, t > 0.