n the two-dividend American call option model, we assume discrete dividends of amount D 1 and D
Question:
n the two-dividend American call option model, we assume discrete dividends of amount D1 and D2 are paid out by the underlying asset at times t1 and t2, respectively. Let S̃t denote the asset price at time t, net of the present value of escrowed dividends and S̃∗t1 (S̃∗t2) denote the optimal exercise price at time t1 (t2) above which the American call should be exercised prematurely. Let r,σ,X and T denote the riskless interest rate, volatility of S̃, strike price and expiration time, respectively. Let C (S̃t,t) denote the value of the American call at time t. Show that S̃∗t1 and S̃∗t2 are given by the solution of the following nonlinear algebraic equations
![where C(S, ) = S [1 - N(a, b; p)] + De-r(12-11) N (a) - X[e-r(t2-t1) N (a) + e-r(T-) N(-a2, b2; -p)] C(S2,](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/5/4/8/754655c50924b07b1700548749898.jpg)
The American call price is given by (Welch and Chen, 1988)
![where C(S, t) = St [1-N3(-f1, -81, -h1; P12, P13, P23)] - X[e-r(ti-t) N (f2) + e-(t2-) N(-f2, 82; -P12)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/5/4/8/789655c50b54f75c1700548786477.jpg)
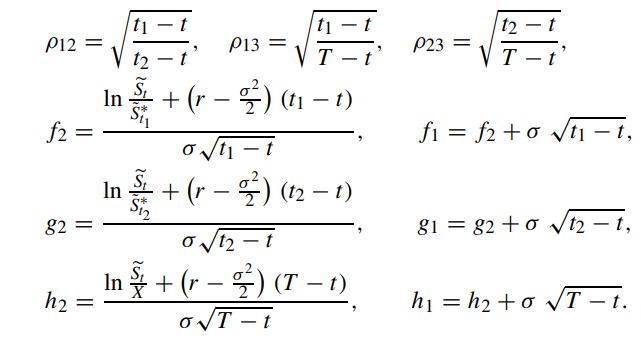
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





