Suppose the dynamics of L_i(t) under the forward measure Q_Tk is governed by (8.3.23), show that the distribution of the LIBOR L_i(T ) under Q_Tk admits the following lognormal approximation (Daniluk and Gataret, 2005):

 

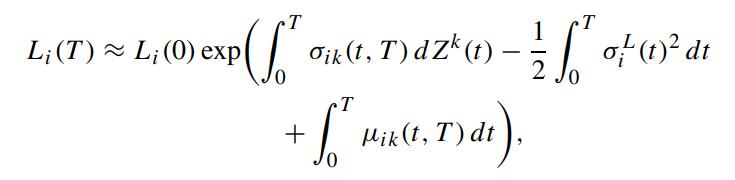
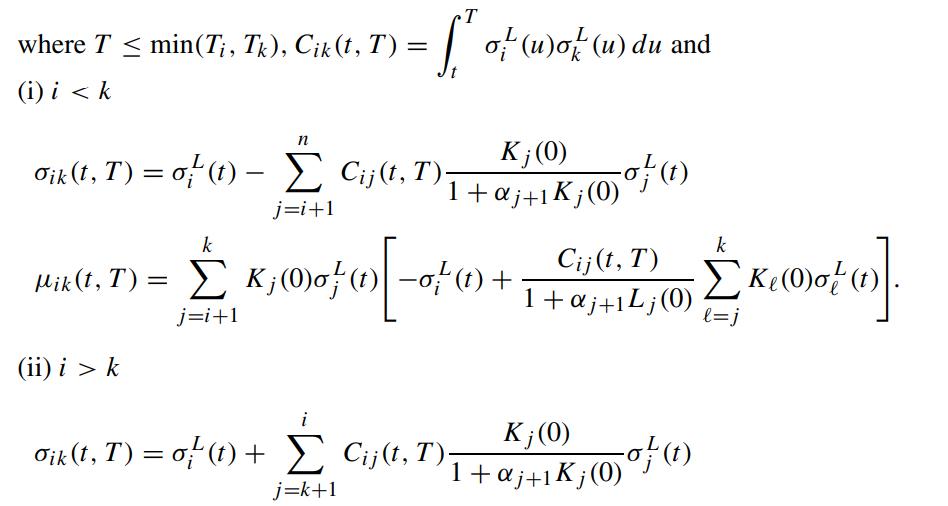
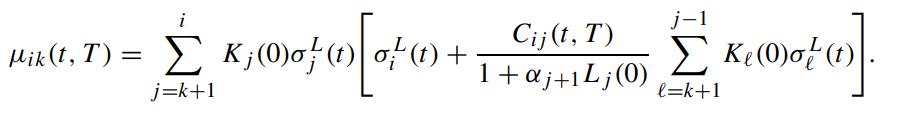
Use integration by parts to show that

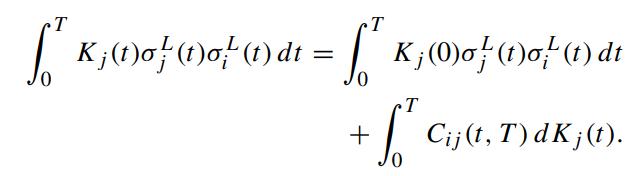Subsequently, show that

Applying the “frozen” LIBOR technique, show that

Transcribed Image Text:

T T L;(T) ≈ L; (0) exp(* %ik (1, T) dz^ (1) of (t)² dt 2 T + ["* mu(1,7) di). S Mik(t, T) 0