Consider a European call bond option maturity on T₀ whose underlying bond pays A_i ≥ 0 at time T_i, 1 ≤ i ≤ n, where 0 0 1 n. Assume that the zero-coupon bond price B(t,T ) follows the one-factor HJM model, where

and the deterministic volatility function satisfies

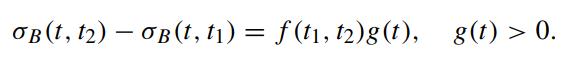
Show that the time-0 price of the European call option on the coupon bearing bond with strike price X is given by (Henrard, 2003)

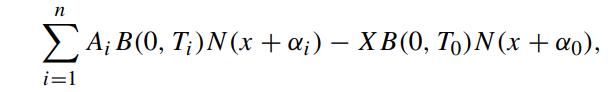where x is the (unique) solution of

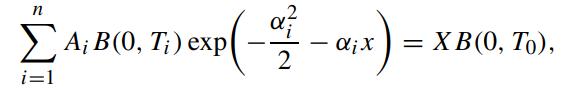
and α_i > 0,i = 0, 1, ··· ,n, is given by

Here, T is the expiration date of the underlying bond.

Transcribed Image Text:

dB(t, T) B(t, T) = =r(t) dt + OB(t, T) dZt,