Suppose the forward LIBOR L(t,T) satisfies the following stochastic differential equation under the risk neutral Q-measure

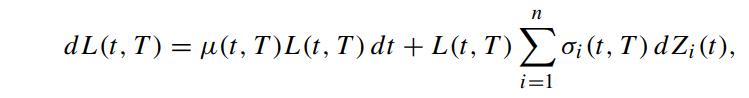where σ_i(t, T), i = 1, 2, ··· ,n are deterministic volatility functions and Z(t) = (Z1(t)···Zn(t))^T is Q-Brownian. Define

which is the time-t price of the T-forward on the T +δ-maturity discount bond. Under the Q_T -measure, show that F_B(t) satisfies

where Z^T (t) = (Z^T₁ (t)···Z^T_n (t))T is Q_T -Brownian. Let V (x,t) denote the forward price of the T-maturity put option on the (T +δ)-maturity bond, where x is the forward bond price. Show that V satisfies

with the terminal condition: V (x,T ) = max(X − x, 0). Here, X is the strike price of the put. Solve for V (x,t) (Miltersen, Sandmann and Sondermann, 1997).

Transcribed Image Text:

n dL(t, T) = µ(t, T)L(t, T) dt +L(t, T) Σo¡(t, T) dZ¡ (t), i=1