Consider the Lognormal LIBOR Market (LLM) model for the LIBOR L_i(t), i = 0, 1, ··· ,n − 1, defined on the tenor structure {T₀,T₁, ··· ,T_n} where 0 0 1 n. Let v_i(t) denote the scalar volatility function of L_i(t), and write L_i(0) = L_i,₀,i = 0, 1, ··· ,n − 1. Now, L_i(t) satisfies

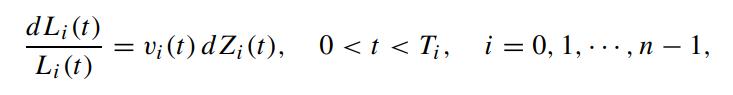
where Z_i(t) is Q_Ti-Brownian. We write ρ_ij (t) as the correlation coefficient between Z_i(t) and Z_j (t) such that ρ_ij (t)dt = dZ_i(t)dZ_j (t). Define

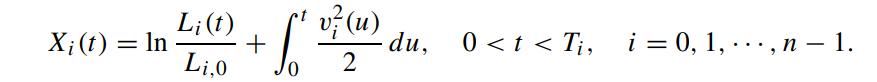
Under the terminal measure Q_Tn , show that X_i(t) satisfies the following stochastic differential equation

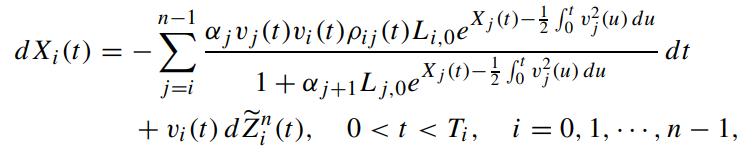with initial condition: X_i(0) = 0, and Z̃_iⁿ⁺¹ (t) is Q_Tn -Brownian under the Girsanov transformation: Q_Ti → Q_Tn.

Note that Z̃ⁿ₁ , ··· ,Z̃ⁿ_n are Q_Tn -Brownian and

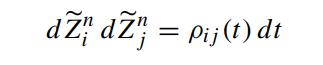
since an equivalent change of a probability measure preserves the correlation between the Brownian processes. We write formally 

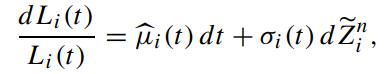
and subsequently μ̂_i(t) is determined. Recall

Transcribed Image Text:

dL; (t) Li(t) = v; (t) dZ; (t), 0 < t < T₁, i = 0, 1,..., n - 1,