Suppose the forward rate as a function of time t evolves as where (t,T ) is a
Question:
Suppose the forward rate as a function of time t evolves as
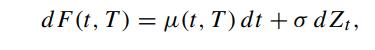
where μ(t,T ) is a deterministic function of t and T . Show that the forward rate is normally distributed, where
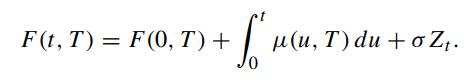
Explain why F(t,T )−F(t,S) is purely deterministic. Deduce that the forward rates at different maturities are perfectly correlated.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
The given forward rate evolution equation is dFtT utT dt dZ where FtT is the forward rate at time t ...View the full answer
Answered By
Asim farooq
I have done MS finance and expertise in the field of Accounting, finance, cost accounting, security analysis and portfolio management and management, MS office is at my fingertips, I want my client to take advantage of my practical knowledge. I have been mentoring my client on a freelancer website from last two years, Currently I am working in Telecom company as a financial analyst and before that working as an accountant with Pepsi for one year. I also join a nonprofit organization as a finance assistant to my job duties are making payment to client after tax calculation, I have started my professional career from teaching I was teaching to a master's level student for two years in the evening.
My Expert Service
Financial accounting, Financial management, Cost accounting, Human resource management, Business communication and report writing. Financial accounting : • Journal entries • Financial statements including balance sheet, Profit & Loss account, Cash flow statement • Adjustment entries • Ratio analysis • Accounting concepts • Single entry accounting • Double entry accounting • Bills of exchange • Bank reconciliation statements Cost accounting : • Budgeting • Job order costing • Process costing • Cost of goods sold Financial management : • Capital budgeting • Net Present Value (NPV) • Internal Rate of Return (IRR) • Payback period • Discounted cash flows • Financial analysis • Capital assets pricing model • Simple interest, Compound interest & annuities
65+ Reviews
86+ Question Solved
Related Book For 
Question Posted:
