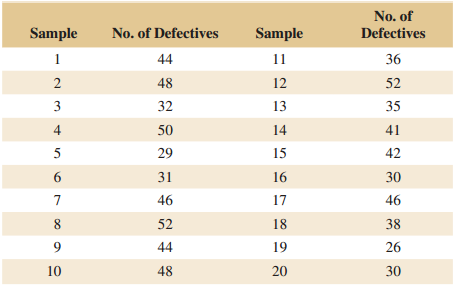
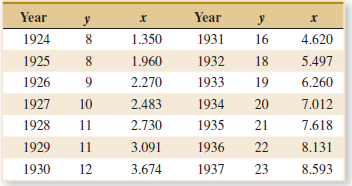
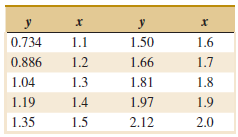
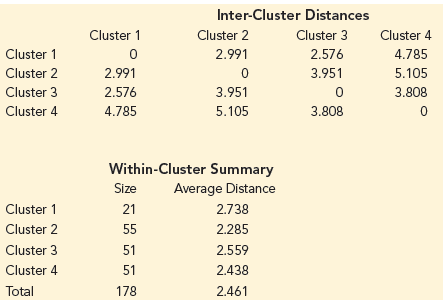
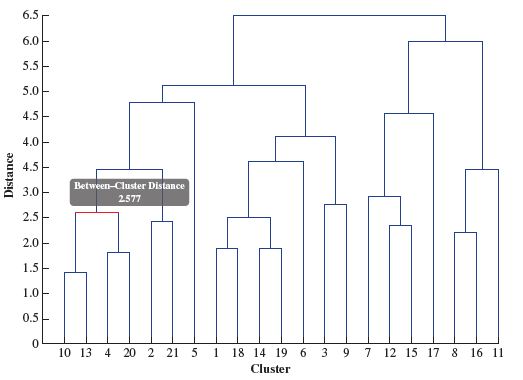
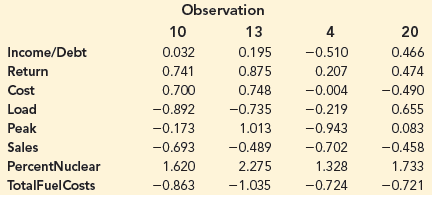
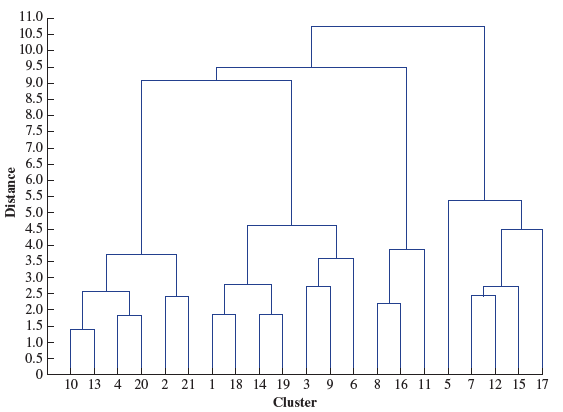
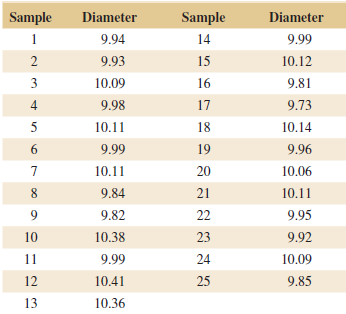
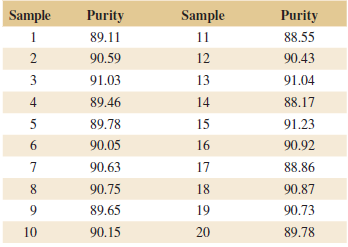
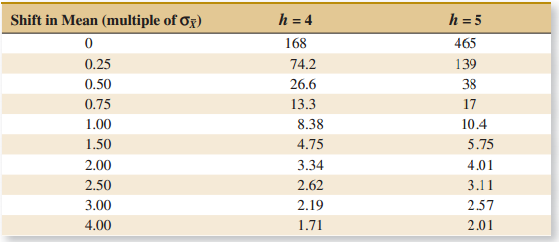
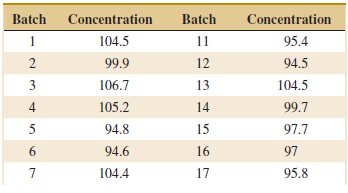
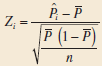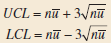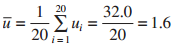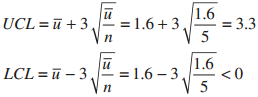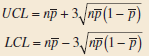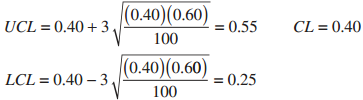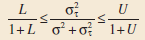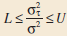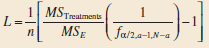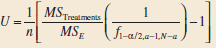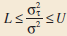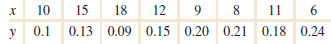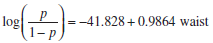Applied Statistics And Probability For Engineers 6th Edition Douglas C. Montgomery, George C. Runger - Solutions
Discover comprehensive solutions and answers key for "Applied Statistics and Probability for Engineers" by Douglas C. Montgomery and George C. Runger. Our online resource provides access to a detailed solution manual, including chapter solutions and step-by-step answers to enhance your understanding. Whether you're looking for solved problems, a test bank, or an instructor manual, our platform offers free download options for solutions in PDF format. Dive into textbook questions and answers with ease, and elevate your learning experience with expertly crafted materials designed for engineering students.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()