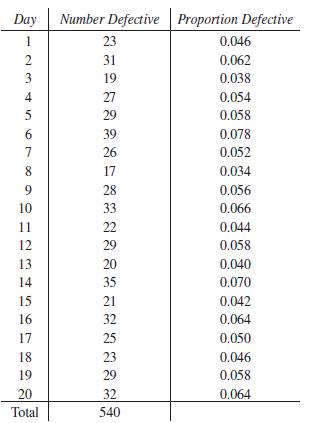
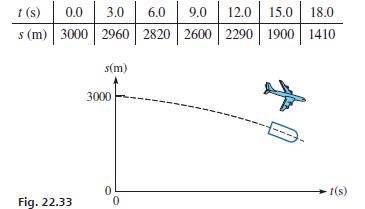
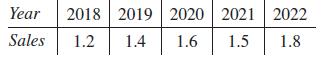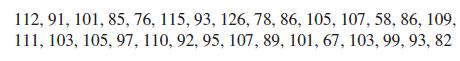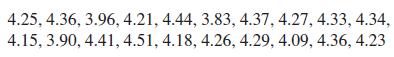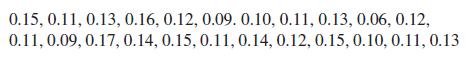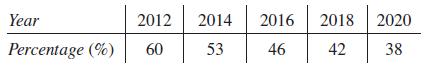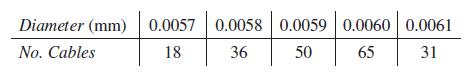Basic Technical Mathematics 12th Edition Allyn J. Washington, Richard Evans - Solutions
Discover comprehensive support for "Basic Technical Mathematics 12th Edition" by Allyn J. Washington and Richard Evans. Enhance your learning experience with our online resources, including an answers key, detailed solutions manual, and a variety of solved problems. Access solutions in PDF format, covering chapter solutions and step-by-step answers to all questions and answers. Our test bank and instructor manual are perfect for educators seeking to enrich their teaching toolkit. Embrace the convenience of a free download to complement your textbook studies and gain clarity on complex mathematical concepts effortlessly.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()