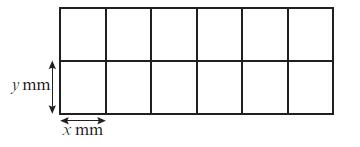
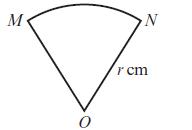
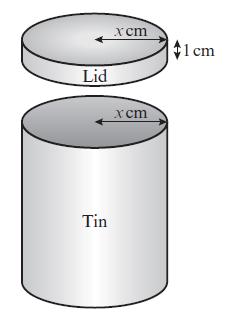
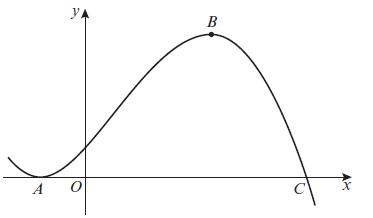
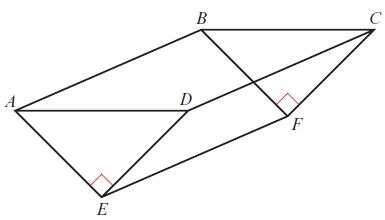
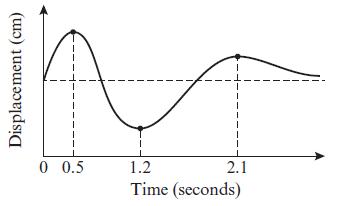
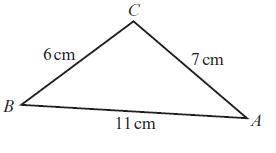
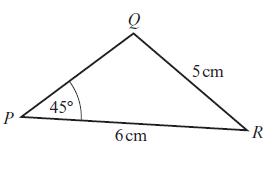
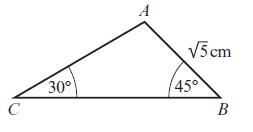
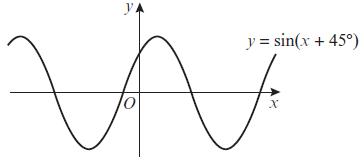
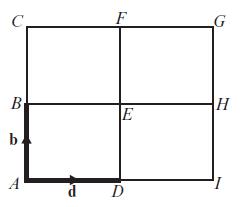
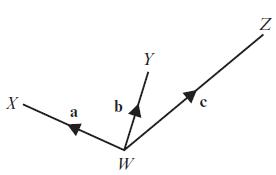
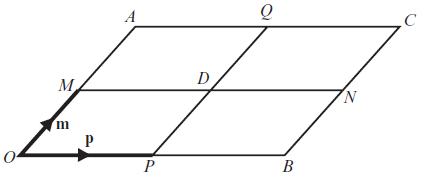
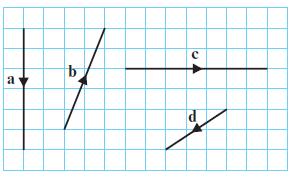
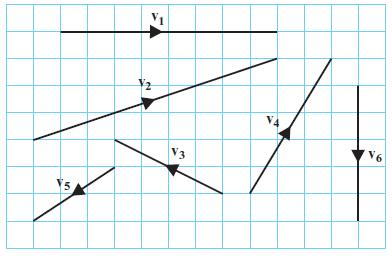
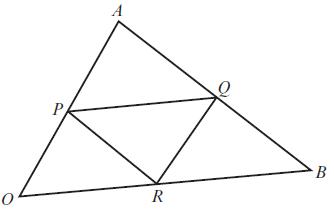
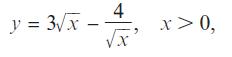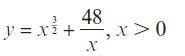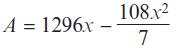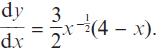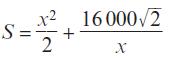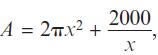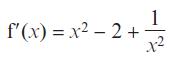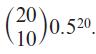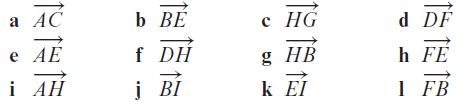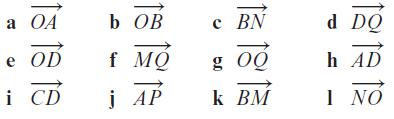Edexcel AS And A Level Mathematics Pure Mathematics Year 1/AS 1st Edition Greg Attwood - Solutions
Discover comprehensive support for "Edexcel AS And A Level Mathematics Pure Mathematics Year 1/AS 1st Edition" by Greg Attwood with our online resource. Dive into a wealth of solved problems and step-by-step answers, designed to enhance your understanding. Access a detailed solution manual and answers key for all chapters, providing concise solutions and insights. Our instructor manual and test bank offer additional practice, ensuring you're well-prepared for exams. Download solutions in PDF format for free, offering convenience and accessibility. Whether you need textbook solutions or chapter answers, find everything you need right here for free download.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()