If z c (t) is a general solution to the complementary equation and zp(t) is a particular
Question:
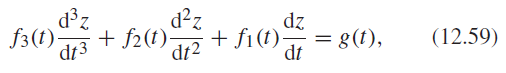
Transcribed Image Text:
d z + f2(t)- dt3 d?z dz + fi(t) (12.59) = g(t), f3(t)- dt2 dt
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 80% (10 reviews)
Since z c satisfies the complem...View the full answer

Answered By

Rishabh Ojha
During my undergraduate i used to participate as TA (Teaching Assistant) in several electronics and computers subject. I'm passionate about learning Computer Science as my bachelors are in Electronics but i learnt most of the Computer Science subjects on my own which Machine Learning also. At Present, i'm a working professional pursuing my career as a Machine Learning Engineer and i want to help others learn during my free hours, that's all the motivation behind giving tuition. To be frank i have no prior experience of tutoring but i have solved problems on opensource platforms like StackOverflow and github. ~Thanks
4.90+
3+ Reviews
10+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Mathematics questions
-
Find the general solution to the system (9.77) for the following matrix pairs: (a) (b) (c) (d) (e) (f) 3 -1 M=(0 3 0 4-2 - 3 2 M= K 2 -1 M= 1200 0 0 6/ -1 3 9 3 -I -1 3 K M= 1311, K= 282 0 1 1
-
Find the general solution to the following second order systems: (a) (b) (c) (d) d2u dr2 d2v dt 10 0 dr 009) 031 du 6 4 LI Ll
-
Find the general solution to the following forced second order systems: (a) (b) (c) (d) (e) (f) (g) du 72 dt2 u=(cos t dr3-23 du 136 5 cos 2r cos 2t u:: (lisin 21 cos t Ll sin 2t cos +1-4 6-11-10 dr2...
-
In five sentences or more answer the following question: Was Japanese Internment necessary to protect Americas national security? Why / why not?
-
If Joan's Grocery Store downsized its operation during the second quarter of 201B and, as a result, paid only $6,119.83 in Form 941 taxes for the quarter that ended on June 30, 201B, should Joan's...
-
Performing vertical analysis Hoosier Optical Company reported the following amounts on its balance sheet at December 31, 2016 and 2015: Prepare a vertical analysis of Hoosier assets for 2016 and...
-
Suppose x is a random variable best described by a uniform probability distribution with c = 20 and d = 45. Find the followmg probabilities: a. ~(20 5 x 5 30) b. ~(20 < x 5 30) c. P(X 2 30) d. ~(x 3...
-
On June 1, 2011, bids were submitted for a construction project to build a new municipal building and fire station. The lowest bid was $5,130,000, submitted by the Shannon Construction Company....
-
please help i can figure out this project i have the journal entry up to adjustments I mainly need help woth the adjusting journal entry and general ledger thats what im stuck on Lenny's Lawn...
-
The Gilster Company, a machine tooling firm, has several plants. One plant, located in St. Cloud, Minnesota, uses a job order costing system for its batch production processes. The St. Cloud plant...
-
Find the solution to the differential equation dy - 2y = xe*. dx dy dx2
-
An nth-order chemical reaction with one reactant obeys the differential equation
-
How would an audit team best evaluate whether the information and communication component is effective at an issuer?
-
1) What are the benefits of home-based working for the company and the employees? 2) What are the challenges in performance management in working from home? 3) What is the right mix of office-based...
-
This assignment is focused on project selection and the underlying factors used to make this determination. You will need to use the readings/videos, the previous learning modules, along with some...
-
1. While improper framing could affect the information we have on sark attacks, I think our decisions come down to "anchoring and adjustment". Because the information we received from the media was...
-
For each of the scenarios in the following table, indicate the most likely reason for the difference in earnings. Scenario Differences in Human Capital Compensating Differential Differences in...
-
All organizations whether it is the government, a private business or small businessman require planning. To turn their dreams of increase in sale, earning high profit and getting success in business...
-
Show that x 4 + 1 is irreducible in Q[x], as we asserted in Example 54.7. Data from in 54.7 Example Consider the splitting field of x 4 + 1 over Q. By Theorem 23.11, we can show that x 4 + 1 is...
-
Using the theoretical sampling strategy, how many samples of size 4 (n = 4) can be drawn from a population of size: (a) N = 5? (b) N = 8? (c) N = 16? (d) N = 50?
-
A 1980 study investigated the relationship between the use of OCs and the development of endometrial cancer [9]. The researchers found that of 117 endometrial-cancer patients, 6 had used the OC...
-
Do these data show a significant association between ethnic origin and genetic type? Ophthalmology Retinitis pigmentosa is a disease that manifests itself via different genetic modes of inheritance....
-
Compute the Kappa statistic and its standard error regarding reproducibility of the diagnosis of dyspnea in this clinic? Pulmonary Disease One important aspect of medical diagnosis is its...
-
Bought an old van for 4000 from Peters promising to pay laterwhat is the transactions
-
Company has a following trade credit policy 1/10 N45. If you can borrow from a bank at 9,5% annual rate, would it be beneficial to borrow money and pay off invoices earlier?
-
Given the following exchange rates, which of the multiple-choice choices represents a potentially profitable inter-market arbitrage opportunity? 129.87/$1.1226/$0.00864/ 114.96/ B $0.8908/ (C)...

Study smarter with the SolutionInn App


