Borel-Cantelli lemma (1) - the direct half. Prove the following theorem. Theorem (Borel-Cantelli lemma). Let ((Omega, mathscr{A},
Question:
Borel-Cantelli lemma (1) - the direct half. Prove the following theorem.
Theorem (Borel-Cantelli lemma). Let \((\Omega, \mathscr{A}, \mathbb{P})\) be a probability space. For every sequence \(\left(A_{i}ight)_{i \in \mathbb{N}} \subset \mathscr{A}\) we have
\[\sum_{i=1}^{\infty} \mathbb{P}\left(A_{i}ight)
[ use Proposition 4.3 (vii) and the fact that \(\mathbb{P}\left(\bigcup_{i \geqslant n} A_{i}ight) \leqslant \sum_{i \geqslant n} \mathbb{P}\left(A_{i}ight)\).]
Remark. This is the 'easy' or direct half of the so-called Borel-Cantelli lemma; for the more difficult part see Theorem 24.9 . The condition \(\omega \in \bigcap_{n=1}^{\infty} \bigcup_{i=n}^{\infty} A_{i}\) means that \(\omega\) happens to be in infinitely many of the \(A_{i}\) and the lemma gives a simple sufficient condition when certain events happen almost surely not infinitely often, i.e. only finitely often with probability one.
(iii) Is there a pathwise connected, open and unbounded set in \(\mathbb{R}\) with finite, strictly positive Lebesgue measure?
Data from proposition 4.3
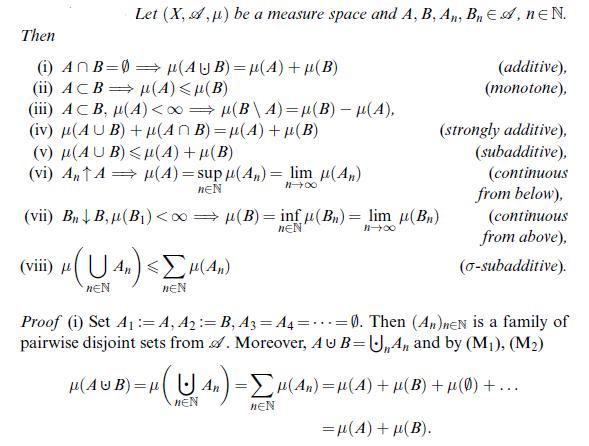
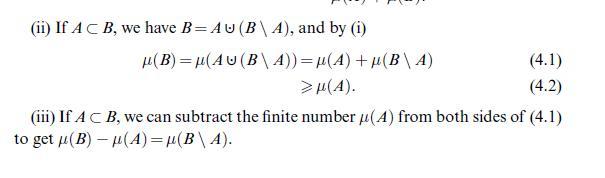


Step by Step Answer:






