Let (lambda=lambda^{1}) be Lebesgue measure on ((mathbb{R}, mathscr{B}(mathbb{R}))). Show that (N in mathscr{B}(mathbb{R})) is a null set
Question:
Let \(\lambda=\lambda^{1}\) be Lebesgue measure on \((\mathbb{R}, \mathscr{B}(\mathbb{R}))\). Show that \(N \in \mathscr{B}(\mathbb{R})\) is a null set if, and only if, for every \(\epsilon>0\) there is an open set \(U_{\epsilon} \supset N\) such that \(\lambda\left(U_{\epsilon}ight)
[ sufficiency is trivial, for necessity use \(\lambda^{*}\) constructed in Theorem 6.1 from \(\left.\lambdaight|_{\mathscr{O}}\) and observe that \(\left.\lambdaight|_{\mathscr{B}\left(\mathbb{R}^{n}ight)}=\left.\lambda^{*}ight|_{\mathscr{B}\left(\mathbb{R}^{n}ight)}\). This gives the required open cover.]
Data from theorem 6.1
![(Carathodory) Let SCP(X) be a semi-ring and u: S [0, ] a pre-measure, i.e. a set function with (i) (0)=0;](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/3/6/76765a9f39f8b5491705636767323.jpg)
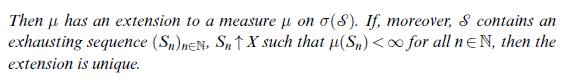
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





