Generalized Fatou lemma. Assume that (left(u_{n}ight)_{n in mathbb{N}} subset mathcal{L}^{1}(mu)). Prove the following. (i) If (u_{n} geqslant
Question:
Generalized Fatou lemma. Assume that \(\left(u_{n}ight)_{n \in \mathbb{N}} \subset \mathcal{L}^{1}(\mu)\). Prove the following.
(i) If \(u_{n} \geqslant v\) for all \(n \in \mathbb{N}\) and some \(v \in \mathcal{L}^{1}(\mu)\), then
\[\int \liminf _{n ightarrow \infty} u_{n} d \mu \leqslant \liminf _{n ightarrow \infty} \int u_{n} d \mu .\]
(ii) If \(u_{n} \leqslant w\) for all \(n \in \mathbb{N}\) and some \(w \in \mathcal{L}^{1}(\mu)\), then
\[\limsup _{n ightarrow \infty} \int u_{n} d \mu \leqslant \int \limsup _{n ightarrow \infty} u_{n} d \mu\]
(iii) Find examples that show that the upper and lower bounds in (i) and (ii) are necessary. [ mimic and scrutinize the proof of Fatou's lemma, especially when it comes to the application of Beppo Levi's theorem. What goes wrong if we do not have this upper/lower bound? Note that we have an 'invisible' \(v=0\) in Theorem 9.11.]
Data from theorem 9.11
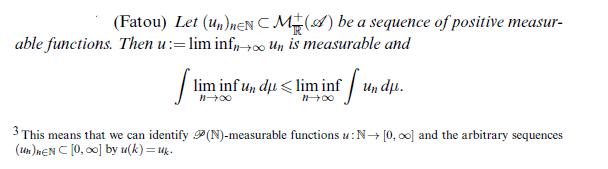
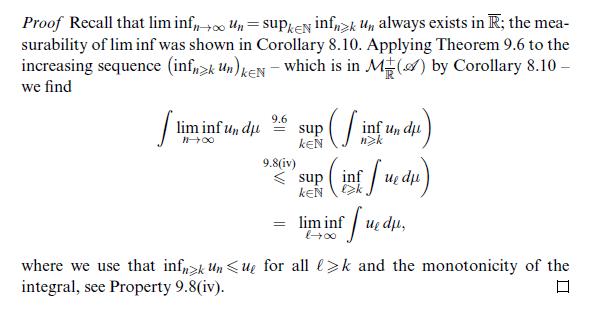
Step by Step Answer:






