Let (mu) be an outer regular measure on ((X, d, mathscr{B}(X)), 1 leqslant p (i) Let (A
Question:
Let \(\mu\) be an outer regular measure on \((X, d, \mathscr{B}(X)), 1 \leqslant p
(i) Let \(A \in \mathscr{B}(X)\) such that \(f=\mathbb{1}_{A} \in \mathcal{L}^{p}(\mu)\). Show that for every \(\epsilon>0\) there is some \(\phi_{\epsilon} \in C_{\mathrm{Lip}}(X)\) such that \(\left\|f-\phi_{\epsilon}ight\|_{p}
(ii) Show that for \(f \in \mathcal{L}^{p}(\mu), f \geqslant 0\), and \(\epsilon>0\) there is some \(\phi_{\epsilon} \in C_{\mathrm{Lip}}(X)\) satisfying \(\left\|f-\phi_{\epsilon}ight\|_{p}
[ use (i) and the sombrero lemma, Theorem 8.8.]
(iii) Show that \(C_{\operatorname{Lip}}(X) \cap \mathcal{L}^{p}(\mu)\) is dense in \(\mathcal{L}^{p}(\mu)\).
Data from theorem 8.8
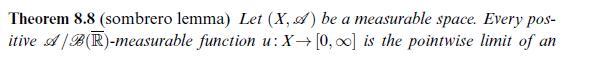

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





