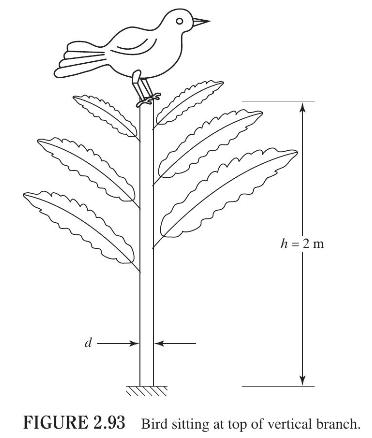
A bird of mass \(m=2 \mathrm{~kg}\) sits at the top of a slender vertical branch of a tree as shown in Fig. 2.93. The height of the branch from the trunk of the tree is \(2 \mathrm{~m}\) and the diameter of the branch is \(d \mathrm{~m}\). The density of the branch is \(700 \mathrm{~kg} / \mathrm{m}^{3}\) and the Young's modulus is \(10 \mathrm{GPa}\).

a. Find the minimum diameter of the branch to avoid buckling under the weight of the bird (by neglecting the weight of the branch). Consider the branch as a fixed free column.

b. Find the natural frequency of vibration of the system (bird on the top of the branch) by treating the branch as a cantilever beam using the diameter found in part (a).

Transcribed Image Text:

d h=2m FIGURE 2.93 Bird sitting at top of vertical branch.