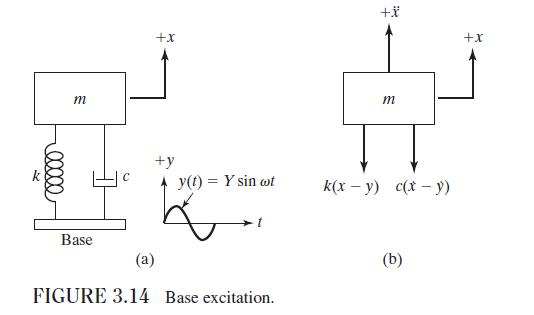
By denoting the amplitudes of relative velocity and relative acceleration of the mass of a viscously damped system subjected to a harmonic base motion, \(y(t)\), as shown in Fig. 3.14, as \(\dot{Z}\) and \(\ddot{Z}\), respectively, find expressions for the ratios \(\frac{\dot{Z}}{\omega_{n} Y}\) and \(\frac{\ddot{Z}}{\omega_{n}^{2} Y}\) in terms of \(r\) and \(\zeta\). The nondimensional ratios \(\frac{\dot{Z}}{\omega_{n} Y}\) and \(\frac{\ddot{Z}}{\omega_{n}^{2} Y}\) are called the relative velocity and relative acceleration frequency responses of the mass, respectively.

Transcribed Image Text:

00000 m +x +X +y m y(t) = Y sin wt k(xy) c(xy) Base (a) K FIGURE 3.14 Base excitation. (b) +x