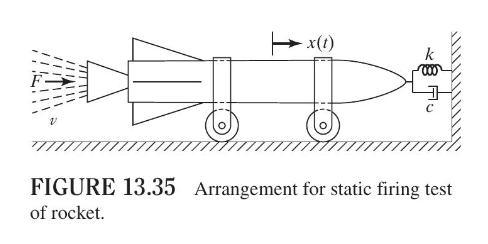
In the static firing test of a rocket, the rocket is anchored to a rigid wall by a nonlinear spring-damper system and fuel is burnt to develop a thrust, as shown in Fig. 13.35. The thrust acting on the rocket during the time period \(0 \leq t \leq t_{0}\) is given by \(F=m_{0} v\), where \(m_{0}\) is the constant rate at which fuel is burned and \(v\) is the velocity of the jet stream. The initial mass of the rocket is \(M\), so that its mass at any time \(t\) is given by \(m=M-m_{0} t, 0 \leq t \leq t_{0}\). The data is: spring force \(=8 \times 10^{5} x+6 \times 10^{3} x^{3} \mathrm{~N}\), damping force \(=10 \dot{x}+20 \dot{x}^{2} \mathrm{~N}, m_{0}=10 \mathrm{~kg} / \mathrm{s}, v=2000 \mathrm{~m} / \mathrm{s}, M=2000 \mathrm{~kg}\), and \(t_{0}=100 \mathrm{~s}\).

(a) Using the Runge-Kutta method of numerical integration, derive the equation of motion of the rocket and

(b) find the variation of the displacement of the rocket. Use Program18 .m.

Transcribed Image Text:

TITTIT -x(t) FIGURE 13.35 Arrangement for static firing test of rocket.