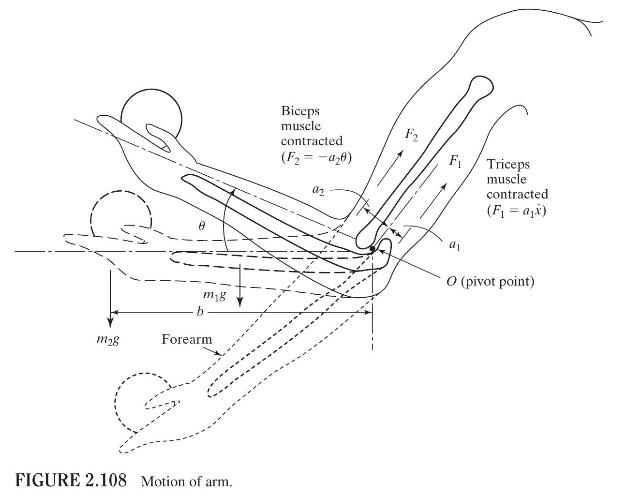
The angular motion of the forearm of a human hand carrying a mass \(m_{0}\) is shown in Fig. 2.108. During motion, the forearm can be considered to rotate about the joint (pivot point) \(O\) with muscle forces modeled in the form of a force by triceps \(\left(c_{1} \dot{x}\right)\) and a force in biceps \(\left(-c_{2} \theta\right)\), where \(c_{1}\) and \(c_{2}\) are constants and \(\dot{x}\) is the velocity with which triceps are stretched (or contracted). Approximating the forearm as a uniform bar of mass \(m\) and length \(l\), derive the equation of motion of the forearm for small angular displacements \(\theta\). Also find the natural frequency of the forearm.

Transcribed Image Text:

mg m28 Forearm FIGURE 2.108 Motion of arm. Biceps muscle contracted (F = -420) F Triceps a2 muscle contracted (F = ax) a O (pivot point)