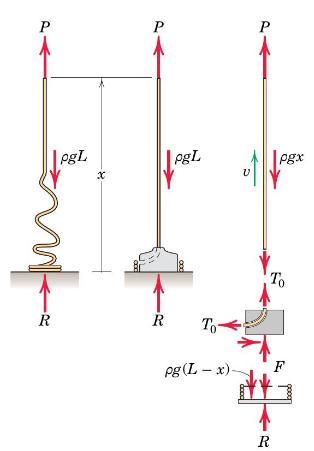
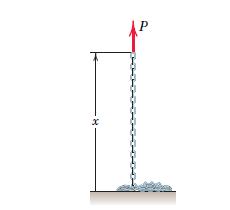
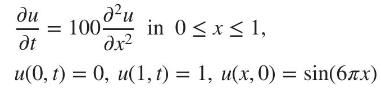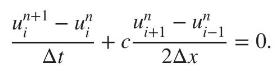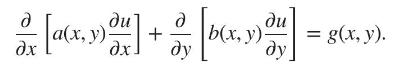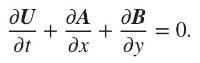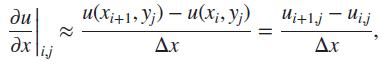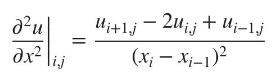Essential Computational Fluid Dynamics 2nd Edition Oleg Zikanov - Solutions

Discover comprehensive insights into "Essential Computational Fluid Dynamics 2nd Edition" by Oleg Zikanov with our extensive collection of questions and answers. Explore our online platform for the answers key and solutions manual, designed to enhance your understanding through detailed solutions PDF and expertly solved problems. Benefit from the test bank and chapter solutions, offering step-by-step answers ideal for both students and instructors. Our instructor manual complements the textbook, providing a resource-rich environment for learning. Experience the convenience of a free download to access these invaluable study tools.