The equation of motion of a spring-mass-damper system subjected to a harmonic force can be expressed as

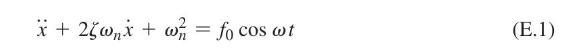
where \(f_{0}=\frac{F_{0}}{m}, \omega_{n}=\sqrt{\frac{k}{m}}\), and \(\zeta=c /\left(2 m \omega_{n}\right)\).

i. Find the steady-state response of the system in the form \(x_{s}(t)=C_{1} \cos \omega t+C_{2} \sin \omega t\) 

ii. Find the total response of the system in the form

Assume the initial conditions of the system as \(x(t=0)=x_{0}\) and \(\dot{x}(t=0)=\dot{x}_{0}\).

Transcribed Image Text:

x + 2wx + w = fo cos wt (E.1)