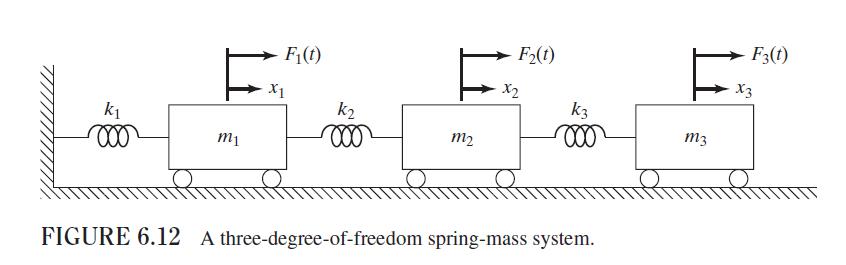
The equations of motion derived using the displacements of the masses, \(x_{1}, x_{2}\), and \(x_{3}\) as degrees of freedom in Fig. 6.12 (Example 6.10) lead to symmetric mass and stiffness matrices in Eq. (E.3) of Example 6.10. Express the equations of motion, (E.3) of Example 6.10, using \(x_{1}, x_{2}-x_{1}\), and \(x_{3}-x_{2}\) as degrees of freedom in the form:

\[[\bar{m}] \ddot{\vec{y}}+[\bar{k}] \vec{y}=\overrightarrow{0}\]

where

\[\vec{y}=\left\{\begin{array}{l}y_{1} \\y_{2} \\y_{3}\end{array}\right\}\]

Show that the resulting mass and stiffness matrices \([\bar{m}]\) and \([\bar{k}]\) are nonsymmetric.

Data From Example 6.10:-

Equation E.3:-

Figure 6.12:-

Transcribed Image Text:

State the free-vibration equations of motion of the system shown in Fig. 6.12.