The Fourier series of a periodic function, (x(t)), is an infinite series given by where (omega) is
Question:
The Fourier series of a periodic function, \(x(t)\), is an infinite series given by
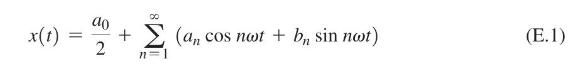
where

\(\omega\) is the circular frequency and \(2 \pi / \omega\) is the time period. Instead of including the infinite number of terms in Eq. (E.1), it is often truncated by retaining only \(k\) terms as
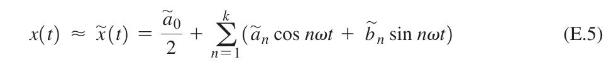
so that the error, \(e(t)\), becomes

Find the coefficients \(\widetilde{a}_{0}, \widetilde{a}_{n}\), and \(\widetilde{b}_{n}\) which minimize the square of the error over a time period:

Compare the expressions of \(\widetilde{a}_{0}, \widetilde{a}_{n}\), and \(\widetilde{b}_{n}\) with Eqs. (E.2)-(E.4) and state your observation(s).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





