The free-vibration solution of a two-degree-of-freedom system can be determined by solving the equations

with \(\vec{x}=\left\{\begin{array}{l}x_{1}(t) \\ x_{2}(t)\end{array}\right\}\), using the initial conditions

If \(\omega_{1}\) and \(\omega_{2}\) are the natural frequencies and \(\vec{u}_{1}\) and \(\vec{u}_{2}\) are the mode shapes of the system obtained from the solution of the characteristic equation

with \(s= \pm \omega_{1}, \pm \omega_{2}\) (characteristic roots), the solution of Eq. (E.1), \(\vec{x}(t)\), can be found as a linear combination of different solutions as:

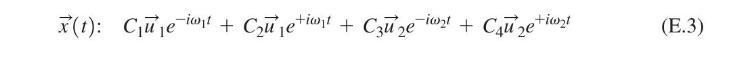
where \(C_{i}, i=1,2,3,4\), are constants. Show that the solution in Eq. (E.3) can be expressed, in equivalent form, as 
where \(A_{1}, A_{2}, \phi_{1}\), and \(\phi_{2}\) are constants.

Transcribed Image Text:

(E.1) 0 = [m]x + [k]x