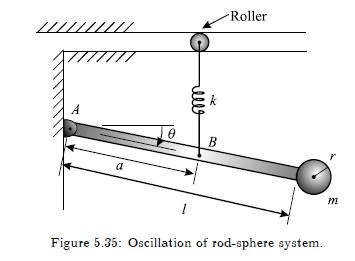
The spring supporting the rod-sphere system in Figure 5.35 is undeformed when the rod is horizontal. Assume the rod mass is negligible. The roller from which the spring is suspended permits the spring to maintain a vertical configuration. If the system is in this position when it is released from rest, derive the equation of motion using

(a) the principle of virtual work along with d'Alembert's principle, and

(b) using Lagrange's equation. Show that the equation of motion is

\[ \begin{gathered} \left(m(l+r)^{2}+\frac{2}{5} m r^{2}\right) \ddot{\theta}+k a^{2} \sin \theta \cos \theta \\ -m g(l+r) \cos \theta=0 \end{gathered} \]

Transcribed Image Text:

/////// A a B Roller Figure 5.35: Oscillation of rod-sphere system. m