The third-order Runge-Kutta formula is given by [vec{X}_{i+1}=vec{X}_{i}+frac{1}{6}left(vec{K}_{1}+4 vec{K}_{2}+vec{K}_{3} ight)] where [begin{gathered}vec{K}_{1}=h vec{F}left(vec{X}_{i}, t_{i} ight) vec{K}_{2}=h vec{F}left(vec{X}_{i}+frac{1}{2} vec{K}_{1}, t_{i}+frac{1}{2} h ight)end{gathered}] and [vec{K}_{3}=h vec{F}left(vec{X}_{i}-vec{K}_{1}+2 vec{K}_{2},

The third-order Runge-Kutta formula is given by

\[\vec{X}_{i+1}=\vec{X}_{i}+\frac{1}{6}\left(\vec{K}_{1}+4 \vec{K}_{2}+\vec{K}_{3}\right)\]

where

\[\begin{gathered}\vec{K}_{1}=h \vec{F}\left(\vec{X}_{i}, t_{i}\right) \\\vec{K}_{2}=h \vec{F}\left(\vec{X}_{i}+\frac{1}{2} \vec{K}_{1}, t_{i}+\frac{1}{2} h\right)\end{gathered}\]

and

\[\vec{K}_{3}=h \vec{F}\left(\vec{X}_{i}-\vec{K}_{1}+2 \vec{K}_{2}, t_{i}+h\right)\]

Using this formula, solve the problem considered in Example 11.2.

Data From Example 11.2:-

Data From Example 11.1:-

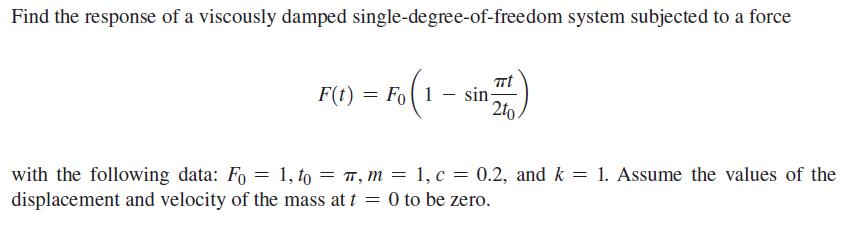
Find the solution of Example 11.1 using the Runge-Kutta method.