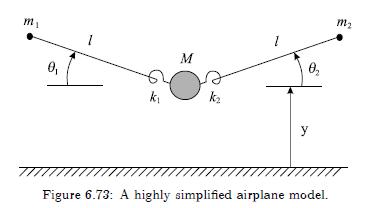
The vibration characteristics of an airplane are very complex due to its intricate system of structures and substructures. Suppose we consider the much simplified model of Figure 6.73, which is a three degree-of-freedom representation of the fuselage and wings. Derive the equations of motion using both Newton's second law and Lagrange's equation. Initially assume arbitrary \(\theta_{1}\) and \(\theta_{2}\). Then consider two simplifications:

(a) symmetrical vibration of the wing-body combination, that is, \(\theta_{1}=\theta_{2}=\theta\), \(m_{1}=m_{2}=m\), and \(K_{1}=K_{2}=K\), and

(b) small \(\theta\). Solve for the free vibration response after simplifying and linearizing the equations of motion. Discuss your assumptions.

Transcribed Image Text:

mi M 1 M k k y Figure 6.73: A highly simplified airplane model.