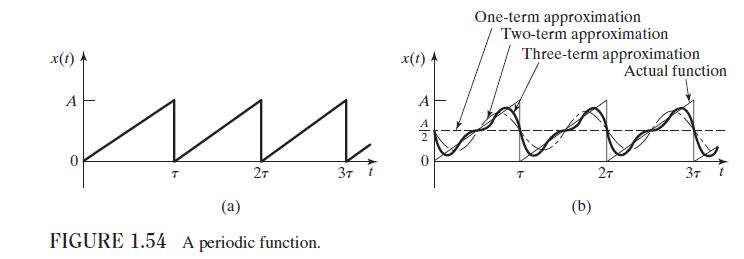
Using the definition given in Problem 1.104, find the rms value of the function shown in Fig. 1.54(a).

Data From Problem 1.104:-

The root mean square (rms) value of a function, \(x(t)\), is defined as the square root of the average of the squared value of \(x(t)\) over a time period \(\tau\) :

\[x_{\mathrm{rms}}=\sqrt{\frac{1}{\tau} \int_{0}^{\tau}[x(t)]^{2} d t}\]

Using this definition, find the rms value of the function

\[x(t)=X \sin \omega t=X \sin \frac{2 \pi t}{\tau}\]

Figure 1.54:-

x(t) A 2T 3T (a) FIGURE 1.54 A periodic function. x(t) A One-term approximation Two-term approximation Three-term approximation Actual function (b) 25 2T 3T