A ball of mass \(m\) and negligible size can slide without friction on the inner wall of a hemisphere of radius \(R=15 \mathrm{~cm}\), as shown in Fig. 7.17. The \(z\) axis shown in figure represents the direction in which gravity acts (downward). At the initial moment, the ball has a horizontal velocity (in the \(x y\) plane) tangent to the wall and its position forms an angle \(\theta_{0}=0.60 \mathrm{rad}\) with the vertical axis. After drawing the forces acting on the mass \(m\), determine the value \(v_{0}\) of the initial speed that is necessary for the ball not to change its altitude during the motion. In case \(m\) has an initial horizontal velocity \(v\) of magnitude greater than \(v_{0}\), it will start moving upwards. To determine:

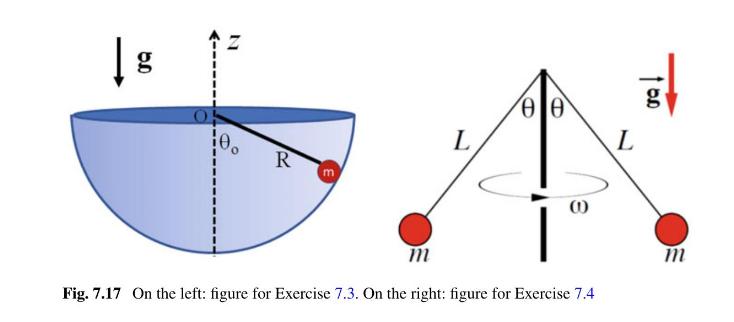
1. the net torque \(\tau\) with respect to the center \(\mathrm{O}\) of the hemisphere and the net force acting on the ball during its motion as a function of the angle \(\theta\);
2. the component \(\boldsymbol{\tau}_{z}\) (that is the component along the z-axis of the torque);
3. the component \(L_{z}\) of the angular momentum, also indicate its properties;
4. the minimum value of \(v_{\min }\) that is necessary for the ball to reach the upper edge of the hemisphere.

Transcribed Image Text:

80 g N R m 100 L L m Fig. 7.17 On the left: figure for Exercise 7.3. On the right: figure for Exercise 7.4 m