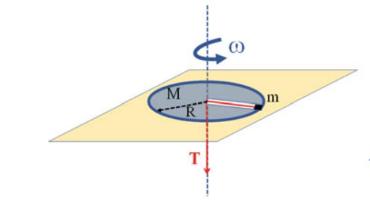
A block of mass \(m=100 \mathrm{~g}\) is constrained to move in a smooth radial groove of a uniform disk of mass \(M=1.00 \mathrm{~kg}\) and radius \(R=10.0 \mathrm{~cm}\). The block is connected to a rope that runs in the groove and passes through a hole in the center of the disk. An external tension \(T\) can be applied to the rope, as in Fig. 12.18. Initially, the disk+block system is in frictionless rotation about a vertical axis passing through the center of the disk and perpendicular to the disk with angular speed \(\omega=10 \mathrm{rad} / \mathrm{s}\). The block initially lies on the edge of the disk.

1. Calculate the tension \(T\) of the string required to keep the block balanced at the edge of the disk.

2. A tension greater than the equilibrium tension is applied to the string and the block approaches the center of the disk. Justify whether, relative to the block+disc system, the following quantities are conserved in the motion: (2.a) linear momentum, (2.b) energy, and (2.c) angular momentum with respect to the axis of rotation.

3. Calculate the angular speed of the disk+block system at the instant when the block is located, stationary in the rotating reference frame with the disk, at distance \(R_{1}=1 / 2 R\) from the center of the disk.

4. Calculate the work done by the string tension in moving the block from the initial position to the position \(R_{1}\).

 Fig. 12.18

Transcribed Image Text:

M R T @ m