(a) Show that for any probability distribution, if we compute the generating function \(Z(\beta) \equiv\left\langle e^{\beta X}\rightangle\) for arbitrary \(\beta\) and \(X\) being the stochastic variable, we can compute all moments using

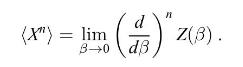
(b) Use the generating function to compute the moments of a Gaussian stochastic variable

(c) Use the generating function to compute the moments of a stochastic variable with uniform probability distribution: \(p(x)=1 /(2 a)\) for \(\left(x_{0}-a\right) \leq x \leq\left(x_{0}+a\right)\), and \(p(x)=0\) otherwise.

Transcribed Image Text:

(X"): = lim B-0 d dB n Z(B).