An approximate way of implementing an (mathrm{RG}) transformation on a square lattice is provided by the so-called
Question:
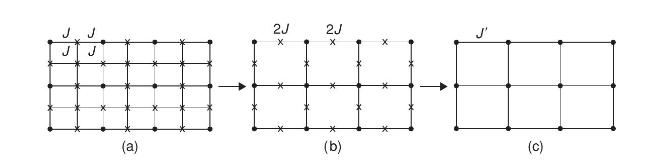
An approximate way of implementing an \(\mathrm{RG}\) transformation on a square lattice is provided by the so-called Migdal-Kadanoff transformation \({ }^{17}\) shown in Figure 14.8. It consists of two essential steps:
(i) First, one-half of the bonds in the lattice are simply removed, so as to change the length scale of the lattice by a factor of 2; to compensate for this, the coupling strength of the remaining bonds is changed from \(J\) to \(2 J\). This takes us from Figure 14.8(a) to Figure 14.8(b).
(ii) Next, the sites marked by crosses in Figure 14.8(b) are eliminated by a set of one-dimensional decimation transformations, leading to Figure 14.8(c) with coupling strength \(J^{\prime}\).
(a) Show that the recursion relation for a spin- \(-\frac{1}{2}\) Ising model on a square lattice, according to the above transformation, is
\[
x^{\prime}=2 x^{2} /\left(1+x^{4}\right),
\]
where \(x=\exp (-2 K)\) and \(x^{\prime}=\exp \left(-2 K^{\prime}\right)\). Disregarding the trivial fixed points \(x^{*}=0\) and \(x^{*}=1\), show that a nontrivial fixed point of this transformation is
\[
x^{*}=\frac{1}{3}\left[-1+2 \sqrt{ } 2 \sinh \left\{\frac{1}{3} \sinh ^{-1} \frac{17}{2 \sqrt{ } 2}\right\}\right] \simeq 0.5437
\]
compare this with the actual value of \(x_{c}\), which is \((\sqrt{ } 2-1) \simeq 0.4142\).
(b) Linearizing around this nontrivial fixed point, show that the eigenvalue \(\lambda\) of this transformation is
\[
\lambda=2\left(1-x^{*}\right) / x^{*} \simeq 1.6785
\]
and hence the exponent \(v=\ln 2 / \ln \lambda \simeq 1.338\); compare this with the actual value of \(v\), which is 1 .
Step by Step Answer:






