The quality factor (Q) of an underdamped oscillator can be defined as where at some time (E)
Question:
The "quality factor" \(Q\) of an underdamped oscillator can be defined as
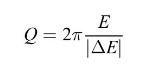
where at some time \(E\) is the total energy of the oscillator and \(|\Delta E|\) is the energy loss in one cycle.
(a) Show that \(Q \simeq \pi / \beta P\), where \(\beta\) is the damping constant and \(P\) is the period of oscillation. Therefore if the damping increases, \(Q\) decreases.
(b) What is \(Q\) for a simple pendulum that loses \(1 \%\) of its energy during each cycle?
(c) The quality factor also describes the sharpness of the resonance curve of a driven, lightly-damped oscillator. Show that to a good approximation \(Q \simeq \omega /(\Delta \omega)\), where \(\Delta \omega\) is the angular frequency difference between the two locations on the amplitude resonance curve for which the amplitude is \(1 / \sqrt{2}\) that at peak resonance.
Step by Step Answer:






