We discovered in the text that the scalar and vector potentials are components of a four vector
Question:
We discovered in the text that the scalar and vector potentials are components of a four vector \(A^{\mu}=(\phi, \mathbf{A})\). In this problem, we will take as given the existence of this four-vector potential \(A^{\mu}\) and, using the known Lorentz transformation of a four-vector and the relations of \(A^{\mu}\) to \(\mathbf{E}\) and \(\mathbf{B}\), we want to derive the Lorentz transformations of \(\mathbf{E}\) and \(\mathbf{B}\). Consider two inertial frames \(\mathcal{O}\) and \(\mathcal{O}^{\prime}\) where \(\mathcal{O}^{\prime}\) is moving with velocity v relative to \(\mathcal{O}\). We split all three-vectors in components parallel and perpendicular to the direction of the Lorentz boost, \(\mathbf{v}\) : for example, we have \(\mathbf{E}=\mathbf{E}_{\|}+\mathbf{E}_{\perp}\). Note that the gradient vector can also be decomposed as \(abla=abla_{\|}+abla_{\perp}\).
(a) First show that \(\mathbf{B}_{\|}^{\prime}=\mathbf{B}_{\|}\).
(b) Show next that \(\boldsymbol{abla}_{\|}^{\prime}=\gamma\left(\boldsymbol{abla}_{\|}+\left(\mathbf{v} / c^{2}\right)(\partial / \partial t)\right)\).
(c) Finally, show that
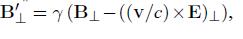
as in the previous problem.
Data from previous problem
Consider two inertial frames \(\mathcal{O}\) and \(\mathcal{O}^{\prime}\) where \(\mathcal{O}^{\prime}\) is moving with velocity \(\mathbf{v}\) relative to \(\mathcal{O}\). We split all three-vectors in components parallel and perpendicular to the direction of the Lorentz boost, \(\mathbf{v}\) : for example, we have \(\mathbf{E}=\mathbf{E}_{\|}+\mathbf{E}_{\perp}\). Show that the Lorentz transformations of the electric and magnetic fields given in the text, equations 8.35 and 8.36 can be written instead as
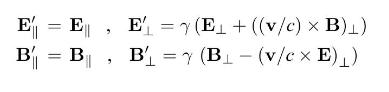
Step by Step Answer:






