Consider the multinomial version of the PCGF test given in (8.23) with (p_{j}) replaced by (widehat{p}_{j}=N^{-1} sum_{i}
Question:
Consider the multinomial version of the PCGF test given in (8.23) with \(p_{j}\) replaced by \(\widehat{p}_{j}=N^{-1} \sum_{i} F_{j}\left(\mathbf{x}_{i}, \widehat{\boldsymbol{\theta}}\right)\). Show that PCGF can be expressed as CGF in (8.27) with \(\widehat{\mathbf{V}}=\operatorname{Diag}\left[N \hat{p}_{i}\right]\). [Conclude that in the multinomial case Andrew's test statistic simplifies to Pearson's statistic.]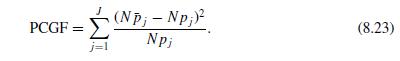
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Microeconometrics Methods And Applications
ISBN: 9780521848053
1st Edition
Authors: A.Colin Cameron, Pravin K. Trivedi
Question Posted:





