Consider the panel GMM estimator of Section 22.2.1. (a) Show that minimization with respect to (beta) of
Question:
Consider the panel GMM estimator of Section 22.2.1.
(a) Show that minimization with respect to \(\beta\) of the quadratic function \(Q_{N}(\beta)\) given after (22.3) yields the panel GMM esimator given after \(Q_{N}(\beta)\) that is expressed using summation notation.
(b) Show that this estimator is equivalent to the estimator defined in (22.4).
(c) For simplicity suppose that the matrices \(\mathbf{Z}\) and \(\mathbf{X}\) in (22.4) are nonstochastic and that \(\mathbf{y}=\mathbf{X} \boldsymbol{\beta}+\mathbf{u}\) where \(\mathbf{u}\) has mean 0 and variance \(\Omega\). Obtain the finite sample variance matrix of the estimator in (22.4) and compare this to the asymptotic results in (22.5).
(d) Simplify the panel GMM estimator in the case that \(r=K\).


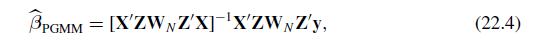
Step by Step Answer:

Microeconometrics Methods And Applications
ISBN: 9780521848053
1st Edition
Authors: A.Colin Cameron, Pravin K. Trivedi





