(a) Derive the time-averaged Navier-Stokes equation (15.13b) from the time dependent form [Eq. (15.11b)], and thereby infer...
Question:
(a) Derive the time-averaged Navier-Stokes equation (15.13b) from the time dependent form [Eq. (15.11b)], and thereby infer the definition (15.13c) for the Reynolds stress. Equation (15.13b) shows how the Reynolds stress affects the evolution of the mean velocity. However, it does not tell us how the Reynolds stress evolves.
(b) Explain why an equation for the evolution of the Reynolds stress must involve averages of triple products of the velocity fluctuation. Similarly, the time evolution of the averaged triple products will involve averaged quartic products, and so on. How do you think you might “close” this sequence of equations (i.e., terminate it at some low order) and get a fully determined system of equations?
(c) Show that the fluctuating part of the Navier-Stokes equation (the difference between the exact Navier-Stokes equation and its time average) takes the following form:
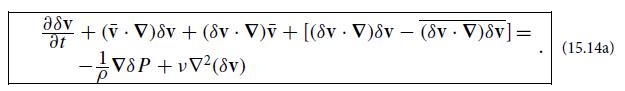
This equation and the fluctuating part of the incompressibility equation
![]()
govern the evolution of the fluctuating variables δv and δP . [The challenge, of course, is to devise ways to solve these equations despite the nonlinearities and the coupling to the mean flow v̅ that show up strongly in Eq. (15.14a).]
(d) By dotting δv into Eq. (15.14a) and then taking its time average, derive the following law for the spatial evolution of the turbulent energy density
![]()
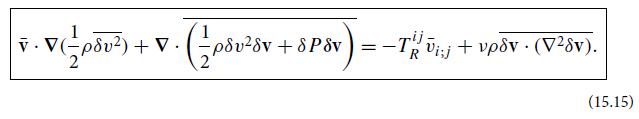
Here
![]()
is the Reynolds stress [Eq. (15.13c)]. Interpret each term in this equation.
(e) Now derive a similar law for the spatial evolution of the energy density of ordered motion, 1/2ρ v̅2. Show that the energy lost by the ordered motion is compensated for by the energy gained by the turbulent motion.
Equations


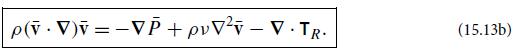

Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





