(a) Express the electromagnetic field tensor as an anti-symmetrized gradient of a 4-vector potential: in slot-naming index notation

Show that, whatever may be the 4-vector potential A(vector, the second of Maxwell’s equations (2.48) is automatically satisfied. Show further that the electromagnetic field tensor is unaffected by a gauge change of the form

where ψ is a scalar field (the generator of the gauge change). Show, finally, that it is possible to find a gauge-change generator that enforces Lorenz gauge

on the new 4-vector potential, and show that in this gauge, the first of Maxwell’s equations (2.48) becomes (in Gaussian units)

(b) Introduce an inertial reference frame, and in that frame split F into the electric and magnetic fields E and B, split  J(vector) into the charge and current densities ρ_e and j, and split the vector potential into a scalar potential and a 3-vector potential

Deduce the 3 + 1 splits of Eqs. (2.51a)–(2.51d), and show that they take the form given in standard textbooks on electromagnetism.

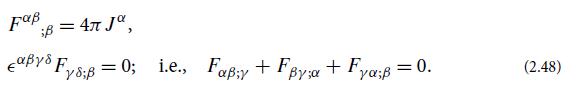
Fa = AB;a - Aa;. (2.51a)