(a) Let a and b be scalar fields with arbitrary but smooth dependence on location in curved...
Question:
(a) Let a and b be scalar fields with arbitrary but smooth dependence on location in curved spacetime, and let A(vector) and B(vector) be vector fields. Show that
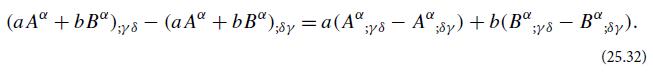
(b) Use Eq. (25.32) to show that
(i) The commutator of the double gradient is independent of how the differentiated vector field varies from point to point and depends only on the value of the field at the location where the commutator is evaluated.
(ii) The commutator is linear in that value. Thereby conclude that there must exist a fourth-rank tensor field R such that Eq. (25.30) is true for any vector field p(vector).
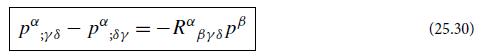
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford
Question Posted:





