(a) Place a local Lorentz frame at the center of Earth, and let jk be the...

(a) Place a local Lorentz frame at the center of Earth, and let ε_jk be the tidal field there, produced by the Newtonian gravitational fields of the Sun and the Moon. For simplicity, treat Earth as precisely spherical. Show that the gravitational acceleration (relative to Earth’s center) at some location on or near Earth’s surface (radius r) is

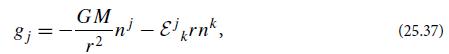
where M is Earth’s mass, and n^j is a unit vector pointing from Earth’s center to the location at which g_j is evaluated.

(b) Show that this gravitational acceleration is minus the gradient of the Newtonian potential

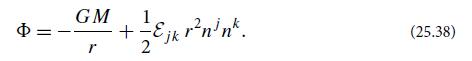
(c) Consider regions of Earth’s oceans that are far from any coast and have ocean depth large compared to the heights of ocean tides. If Earth were nonrotating, then explain why the analysis of Sec. 13.3 predicts that the ocean surface in these regions would be a surface of constant Φ. Explain why this remains true to good accuracy also for the rotating Earth.

(d) Show that in these ocean regions, the Moon creates high tides pointing toward and away from itself and low tides in the transverse directions on Earth; and similarly for the Sun. Compute the difference between high and low tides produced by the Moon and by the Sun, and the difference of the total tide when the Moon and the Sun are in approximately the same direction in the sky. Your answers are reasonably accurate for deep-ocean regions far from any coast, but near a coast, the tides are typically larger and sometimes far larger, and they are shifted in phase relative to the positions of the Moon and Sun. Why?

Transcribed Image Text:

8j GM r.2 -n³ - Ej krnk, (25.37)