Since Maxwells equations, written in terms of the classically measurable electromagnetic field tensor F [Eqs. (2.48)] involve
Question:
Since Maxwell’s equations, written in terms of the classically measurable electromagnetic field tensor F [Eqs. (2.48)] involve only single gradients, it is reasonable to expect them to be lifted into curved spacetime without curvature-coupling additions. Assume this is true. It can be shown that:
(i) If one writes the electromagnetic field tensor F in terms of a 4-vector potential A(vector) as
![]()
then half of the curved-spacetime Maxwell equations, Fαβ;γ + Fβγ;α + Fγα;β = 0 [the second of Eqs. (2.48)] are automatically satisfied
(ii) F is unchanged by gauge transformations in which a gradient is added to the vector potential,
![]()
(iii) By such a gauge transformation one can impose the Lorenz-gauge condition ∇(vector) · A(vector) = 0 on the vector potential.
Show that, when the charge-current 4-vector vanishes, J(vector) = 0, the other half of the Maxwell equations, Fαβ;β = 0 [the first of Eqs. (2.48)] become, in Lorenz gauge and in curved spacetime, the wave equation with curvature coupling [Eq. (25.60)].
Eq. 25.60

Equation 2.48.
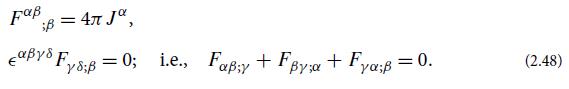
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





