On the surface of a sphere, such as Earth, introduce spherical polar coordinates in which the metric,
Question:
On the surface of a sphere, such as Earth, introduce spherical polar coordinates in which the metric, written as a line element, takes the form
![]()
where a is the sphere’s radius.
(a) Show (first by hand and then by computer) that the connection coefficients for the coordinate basis {∂/∂θ , ∂/∂∅} are
![]()
(b) Show that the symmetries (25.45) of the Riemann tensor guarantee that its only nonzero components in the above coordinate basis are
![]()
(c) Show, first by hand and then by computer, that
![]()
(d) Show that in the basis
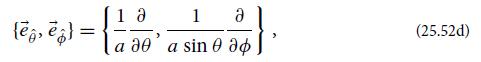
the components of the metric, the Riemann tensor, the Ricci tensor, the curvature scalar, and the Weyl tensor are
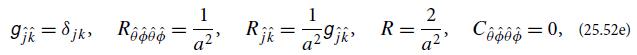
respectively. The first of these implies that the basis is orthonormal; the rest imply that the curvature is independent of location on the sphere, as it should be by spherical symmetry. [The θ dependence in the coordinate components of Riemann, Eq. (25.52c), like the θ dependence in the metric component g∅∅, is a result of the θ dependence in the length of the coordinate basis vector e∅(vector) : |e∅(vector)| = a sin θ.]
Equation 25.45.
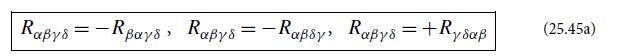
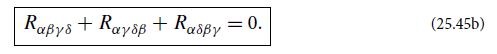
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





