Consider two neighboring geodesics (great circles) on a sphere of radius a, one the equator and the
Question:
Consider two neighboring geodesics (great circles) on a sphere of radius a, one the equator and the other a geodesic slightly displaced from the equator (by △θ = b) and parallel to it at ∅ = 0. Let ξ(vector) be the separation vector between the two geodesics, and note that at ∅ = 0, ξ(vector) = b∂/∂θ. Let l be proper distance along the equatorial geodesic, so d/dl = u(vector) is its tangent vector.
(a) Show that l = a∅ along the equatorial geodesic.
(b) Show that the equation of geodesic deviation (25.31) reduces to
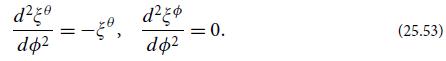
(c) Solve Eq. (25.53), subject to the above initial conditions, to obtain
![]()
Verify, by drawing a picture, that this is precisely what one would expect for the separation vector between two great circles.
Equation (25.31)
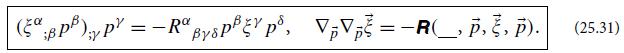
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





